
"Teorema Pythagoras" dinamakan oleh ahli matematika Yunani kuno yaitu Pythagoras, yang dianggap sebagai orang yang pertama kali memberikan bukti teorema ini. Akan tetapi, banyak orang yang percaya bahwa terdapat hubungan khusus antara sisi dari sebuah segi tiga siku-siku jauh sebelum Pythagoras menemukannya.
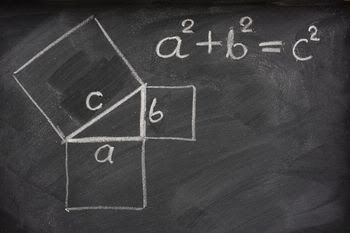
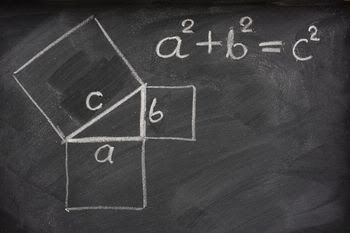
Teorema Pythagoras memainkan peran yang sangat signifikan dalam berbagai bidang yang berkaitan dengan matematika. Misalnya, untuk membentuk dasar trigonometri dan bentuk aritmatika, di mana bentuk ini menggabungkan geometri dan aljabar. Teorema ini adalah sebuah hubungan dalam Geometri Euclides di antara tiga sisi dari segi tiga siku-siku. Hal ini menyatakan bahwa 'Jumlah dari persegi yang dibentuk dari panjang dua sisi siku-sikunya akan sama dengan jumlah persegi yang dibentuk dari panjang hipotenusa-nya'.
Secara matematis, teorema ini biasanya biasanya ditulis sebagai : a2 + b2 = c2 , di mana a dan b mewakili panjang dari dua sisi lain dari segitiga siku-siku dan c mewakili panjang dari hipotenusanya (sisi miring).
Sejarah Teorema Pythagoras
Sejarah dari Teorema Pythagoras dapat dibagi sebagai berikut:
1. pengetahuan dari Triple Pythagoras,
2. hubungan antara sisi-sisi dari segitiga siku-siku dan sudut-sudut yang berdekatan, 3. bukti dari teorema.
Sekitar 4000 tahun yang lalu, orang Babilonia dan orang Cina telah menyadari fakta bahwa sebuah segitiga dengan panjang sisi 3, 4, dan 5 harus merupakan segitiga siku-siku. Mereka menggunakan konsep ini untuk membangun sudut siku-siku dan merancang segitiga siku-siku dengan membagi panjang tali ke dalam 12 bagian yang sama, seperti sisi pertama pada segitiga adalah 3, sisi kedua adalah 4, dan sisi ketiga adalah 5 satuan panjang.
Sekitar 2500 tahun SM, Monumen Megalithic di Mesir dan Eropa Utara terdapat susunan segitiga siku-siku dengan panjang sisi yang bulat. Bartel Leendert van der Waerden meng-hipotesis-kan bahwa Tripel Pythagoras diidentifikasi secara aljabar. Selama pemerintahan Hammurabi the Great (1790 - 1750 SM), tablet Plimpton Mesopotamian 32 terdiri dari banyak tulisan yang terkait dengan Tripel Pythagoras. Di India (Abad ke-8 sampai ke-2 sebelum masehi), terdapat Baudhayana Sulba Sutra yang terdiri dari daftar Tripel Pythagoras yaitu pernyataan dari dalil dan bukti geometris dari teorema untuk segitiga siku-siku sama kaki.
Pythagoras (569-475 SM) menggunakan metode aljabar untuk membangun Tripel Pythagoras. Menurut Sir Thomas L. Heath, tidak ada penentuan sebab dari teorema ini selama hampir lima abad setelah Pythagoras menuliskan teorema ini. Namun, penulis seperti Plutarch dan Cicero mengatributkan teorema ke Pythagoras sampai atribusi tersebut diterima dan dikenal secara luas. Pada 400 SM, Plato mendirikan sebuah metode untuk mencari Tripel Pythagoras yang baik dipadukan dengan aljabar and geometri. Sekitar 300 SM, elemen Euclid (bukti aksiomatis yang tertua) menyajikan teorema tersebut. Teks Cina Chou Pei Suan Ching yang ditulis antara 500 SM sampai 200 sesudah masehi memiliki bukti visual dari Teorema Pythagoras atau disebut dengan "Gougu Theorem" (sebagaimana diketahui di Cina) untuk segitiga berukuran 3, 4, dan 5. Selama Dinasti Han (202 SM - 220 M), Tripel Pythagoras muncul di Sembilan Bab pada Seni Mathematika seiring dengan sebutan segitiga siku-siku. Rekaman pertama menggunakan teorema berada di Cina sebagai 'theorem Gougu', dan di India dinamakan "Bhaskara theorem".
Namun, hal ini belum dikonfirmasi apakah Pythagoras adalah orang pertama yang menemukan hubungan antara sisi dari segitiga siku-siku, karena tidak ada teks yang ditulis olehnya yang ditemukan. Walaupun demikian, nama Pythagoras telah dipercaya untuk menjadi nama yang sesuai untuk teorema ini.
Bagaimana dengan bukti teorema menurut Pythagoras?
Secara matematis, teorema ini biasanya biasanya ditulis sebagai : a2 + b2 = c2 , di mana a dan b mewakili panjang dari dua sisi lain dari segitiga siku-siku dan c mewakili panjang dari hipotenusanya (sisi miring).
Sejarah Teorema Pythagoras
Sejarah dari Teorema Pythagoras dapat dibagi sebagai berikut:
1. pengetahuan dari Triple Pythagoras,
2. hubungan antara sisi-sisi dari segitiga siku-siku dan sudut-sudut yang berdekatan, 3. bukti dari teorema.
Sekitar 4000 tahun yang lalu, orang Babilonia dan orang Cina telah menyadari fakta bahwa sebuah segitiga dengan panjang sisi 3, 4, dan 5 harus merupakan segitiga siku-siku. Mereka menggunakan konsep ini untuk membangun sudut siku-siku dan merancang segitiga siku-siku dengan membagi panjang tali ke dalam 12 bagian yang sama, seperti sisi pertama pada segitiga adalah 3, sisi kedua adalah 4, dan sisi ketiga adalah 5 satuan panjang.
Sekitar 2500 tahun SM, Monumen Megalithic di Mesir dan Eropa Utara terdapat susunan segitiga siku-siku dengan panjang sisi yang bulat. Bartel Leendert van der Waerden meng-hipotesis-kan bahwa Tripel Pythagoras diidentifikasi secara aljabar. Selama pemerintahan Hammurabi the Great (1790 - 1750 SM), tablet Plimpton Mesopotamian 32 terdiri dari banyak tulisan yang terkait dengan Tripel Pythagoras. Di India (Abad ke-8 sampai ke-2 sebelum masehi), terdapat Baudhayana Sulba Sutra yang terdiri dari daftar Tripel Pythagoras yaitu pernyataan dari dalil dan bukti geometris dari teorema untuk segitiga siku-siku sama kaki.
Pythagoras (569-475 SM) menggunakan metode aljabar untuk membangun Tripel Pythagoras. Menurut Sir Thomas L. Heath, tidak ada penentuan sebab dari teorema ini selama hampir lima abad setelah Pythagoras menuliskan teorema ini. Namun, penulis seperti Plutarch dan Cicero mengatributkan teorema ke Pythagoras sampai atribusi tersebut diterima dan dikenal secara luas. Pada 400 SM, Plato mendirikan sebuah metode untuk mencari Tripel Pythagoras yang baik dipadukan dengan aljabar and geometri. Sekitar 300 SM, elemen Euclid (bukti aksiomatis yang tertua) menyajikan teorema tersebut. Teks Cina Chou Pei Suan Ching yang ditulis antara 500 SM sampai 200 sesudah masehi memiliki bukti visual dari Teorema Pythagoras atau disebut dengan "Gougu Theorem" (sebagaimana diketahui di Cina) untuk segitiga berukuran 3, 4, dan 5. Selama Dinasti Han (202 SM - 220 M), Tripel Pythagoras muncul di Sembilan Bab pada Seni Mathematika seiring dengan sebutan segitiga siku-siku. Rekaman pertama menggunakan teorema berada di Cina sebagai 'theorem Gougu', dan di India dinamakan "Bhaskara theorem".
Namun, hal ini belum dikonfirmasi apakah Pythagoras adalah orang pertama yang menemukan hubungan antara sisi dari segitiga siku-siku, karena tidak ada teks yang ditulis olehnya yang ditemukan. Walaupun demikian, nama Pythagoras telah dipercaya untuk menjadi nama yang sesuai untuk teorema ini.
Teorema Pythagoras menurut bangsa India
Di India (abad ke-8 sampai ke-2 sebelum masehi),terdapat Baudhayana Sutra yang terdiri dari daftar Triple Pythagoras yaitu pernyataan dari dalil dan bukti geometris dari teorema untuk segitiga siku-siku sama kaki. Teorema Pythagoras ini dikenal dengan nama Teorema Bhaskara. India Baudhâyana adalah seorang imam dan matematikawan yang hidup sekitar 800-600 SM. Dia mungkin tidak tertarik pada matematika untuk kepentingan sendiri tetapi untuk penggunaannya dalam pembangunan altar diperlukan untuk berkorban kepada dewa-dewa dan ritual keagamaan lainnya. Untuk ces sacrifi ini menjadi sukses dan para dewa mengabulkan keinginan rakyat kesehatan yang baik, kelimpahan makanan, dan sebagainya, mezbah harus dibangun menurut pengukuran sangat tepat. Baudhâyana’s Sulba Sutra atau ‘Rule of Chords,’ ditulis dalam bahasa Sanskerta dan matematika tanpa menggunakan simbol-simbol, adalah kumpulan dari hasil matematika dan geometri con-instruksi menyatakan tanpa bukti. Di antara ini, kita menemukan pernyataan berikut. “Dia mencari-cari melalui surat-surat. “Di sini kita adalah: tali terbentang sepanjang diagonal menghasilkan suatu wilayah yang vertikal dan horisontal sisi membuat bersama-sama.” Ini dasarnya bentuk umum dari apa yang kita sebut teorema Pythagoras.
Bukti Teorema Pythagoras menurut Bangsa India
Bukti Teorema Pythagoras menurut Bangsa India
Luas Daerah persegi jika gambar di bawah adalah C × C atau C2,
dimana area persegi luar adalah, (A + B)2= A2+ B2+ 2 AB. Di sisi lain seseorang dapat menemukan daerah alun-alun luar sebagai berikut: Daerah luar persegi = Luas persegi batin + Jumlah dari daerah dari empat tepat segitiga di sekitar alun-alun bagian dalam, oleh karena itu
A2 + B2 + 2 AB = C2 + 4 1/2 AB, atau A2 + B2 = C2
Gambar: Bukti Teorema Pythagoras Berdasarkan bangsa Indian
Bagaimana dengan bukti teorema menurut Pythagoras?
Dia harus terlebih dahulu menjelaskan pengertian tentang apa yang pada zamannya merupakan sebuah bukti matematika. berarti awalnya “untuk membuat kebenaran (atau kesalahan) dari sebuah pernyataan matematika terlihat. contoh pengajaran matematika di zaman kuno yang tampaknya mendukung dugaan kami. Ini adalah bagian dari Plato’s Meno di mana Socrates bertanya seorang budak bagaimana luas persegi dengan panjang sisi dua unit dapat digandakan tanpa mengubah bentuknya. Dia kemudian menggambar diagram [lihat gambar (1)] menunjukkan alun-alun yang menjadi dua kali lipat. Setelah budak jawaban bahwa kuadrat barangkali akan berlipat ganda dengan menggandakan panjang sisi-sisinya, Sokrates menggambar ond detik-diagram (2) untuk menunjukkan bahwa persegi yang sisinya dua kali lebih lama sebagai orang-orang yang asli, memiliki luas wilayah empat kali ukurannya. Dia kemudian melanjutkan untuk menggambar diagram ketiga (3) menunjukkan bahwa sebuah persegi yang sisi panjang tiga unit, memiliki luas wilayah persegi sembilan unit, dan karenanya tidak dapat ganda yang asli. Akhirnya dalam diagram keempat (4) ia menunjukkan bahwa pada diagonal persegi telah tepat dua kali daerah asli.
Proposisi yang telah digambarkan dan “terbukti” di atas, dapat diformulasikan sebagai berikut: “Sebuah persegi dibangun di diagonal lain telah dua kali daerah yang lain.” Jadi pada diagonal persegi adalah persegi pada sisi miring, dan Socrates menunjukkan bahwa daerah ini dua kali lipat persegi yang asli, dengan kata lain, sama dengan jumlah dari kuadrat pada kedua sisi lainnya.
sumber:
http://library-math.unm.ac.id/blog/?p=220
http://math07.findtalk.net/t38-sejarah-singkat-teorema-pythagoras
sumber:
http://library-math.unm.ac.id/blog/?p=220
http://math07.findtalk.net/t38-sejarah-singkat-teorema-pythagoras
Tidak ada komentar:
Posting Komentar